As shown in the previous chapters the general solution for the acoustic pressure can be written as
with
for the classical solution, and
for the Gaussian beam approximation.
Either expression does not take into account the dissipation of energy due to material absorption,
and due to the transfer of energy every time the acoustic wave bounces on a boundary.
Such dissipation is frequency-dependent (and more relevant as frequency increases),
and implies using a corrected amplitude 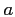 ,
which corresponds to the original amplitude,
multiplied by two decaying factors
,
which corresponds to the original amplitude,
multiplied by two decaying factors 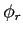 and
and 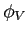 :
:
where 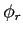 and
and 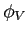 stand, respectively,
for the decay due to boundary reflections, and due to volume absorption.
Both factors are described in the following sections.
stand, respectively,
for the decay due to boundary reflections, and due to volume absorption.
Both factors are described in the following sections.
Subsections
Orlando Camargo Rodríguez
2012-06-21
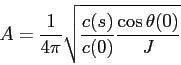
![\begin{displaymath}A = \frac {1}{4\pi}\sqrt{ \frac {c(s)}{c(0)} \frac {\cos\thet...
...
\exp\left[ -\frac{1}{2}i\omega \frac {p(s)}{q(s)} n^2 \right] \end{displaymath}](img171.png)