Eigenray search is perhaps one of the most difficult problems to tackle within the context of ray tracing.
Stated simply as the task of calculating a set of rays,
which connect the source to the receiver,
it is important to keep in mind that in general rays can be sent backwards to the source.
Therefore,
if a ray misses the receiver when propagating forward it still has the chance to hit the receiver on its way back
to the source.
Further complications arise when the rays can be absorbed by the boundaries,
or when small variations of the launching angle lead to non-linear variations of ray trajectories
(a situation, typical of the placing of objects inside the waveguide).
In order to provide a robust method of eigenray search TRACEO uses two different
approaches to the problem,
namely:
- If all rays are propagating forwards,
TRACEO interpolates ray depth at each array range for every launching angle.
This procedure generates a matrix of the form:
where 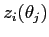 represents ray depth at range
represents ray depth at range 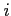 and launching angle
and launching angle 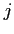 .
Then, at the
.
Then, at the 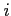 th range, with the hydrophone located at depth
th range, with the hydrophone located at depth 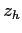 ,
TRACEO calculates the function
,
TRACEO calculates the function
using the correspond row of the matrix;
if an eigenray exists in the interval 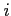 and
and 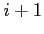 ,
the function
,
the function 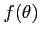 will switch signs between
will switch signs between 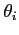 and
and 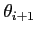 ;
in such case the Regula Falsi method is used to find the zero of the function.
Once the zero is found the ray is calculated,
and written to the output file as an eigenray.
In order to avoid an infinite loop the eigenray search is interrupted if the number of iterations
is greater than a given limit.
Particular care is taken in order to deal with rays,
which for any reason do not reach the given array range.
The search is interrupted if a ``returning'' ray is detected.
The Regula Falsi method is computationally accurate and efficient,
as long as the function
;
in such case the Regula Falsi method is used to find the zero of the function.
Once the zero is found the ray is calculated,
and written to the output file as an eigenray.
In order to avoid an infinite loop the eigenray search is interrupted if the number of iterations
is greater than a given limit.
Particular care is taken in order to deal with rays,
which for any reason do not reach the given array range.
The search is interrupted if a ``returning'' ray is detected.
The Regula Falsi method is computationally accurate and efficient,
as long as the function 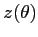 can be properly computed,
which won't be the case for returning rays.
can be properly computed,
which won't be the case for returning rays.
- As an alternative to the previous method TRACEO can use a less accurate (but stable)
search of eigenrays by proximity.
At each range ray depth
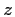 is calculated,
and for each depth (if there is more than one) TRACEO calculates the difference
is calculated,
and for each depth (if there is more than one) TRACEO calculates the difference
where 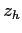 represents hydrophone depth;
if the difference is less than a given threshold TRACEO writes the ray to the output file
as an eigenray.
Certainly,
the accuracy of the method depends on the choice of the threshold,
and on the number of launching angles
(the more, the better).
Until a better approach is idealized for dealing with returning rays the proximity method seems to offer
a reasonable compromise between accuracy and stability.
represents hydrophone depth;
if the difference is less than a given threshold TRACEO writes the ray to the output file
as an eigenray.
Certainly,
the accuracy of the method depends on the choice of the threshold,
and on the number of launching angles
(the more, the better).
Until a better approach is idealized for dealing with returning rays the proximity method seems to offer
a reasonable compromise between accuracy and stability.
Eigenrays are not grouped by TRACEO according the coordinates of the array;
they are witten progressively, one after another, to the output file.
It is up to the user to group them according to the position of each hydrophone.
Orlando Camargo Rodríguez
2012-06-21
![\begin{displaymath}
\left[
\begin{array}{cccccc}
& r_1 & r_2 & r_3 & \ldots & ...
... & z_3(\theta_n) & \ldots & z_m(\theta_n)
\end{array} \right]
\end{displaymath}](img280.png)