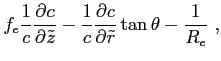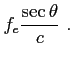The equations from section A.4 can be easily extended in order to account for earth's curvature,
and correspond to[15]:
where 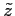 lies along the radius of the earth,
lies along the radius of the earth,
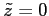 at the surface,
at the surface,
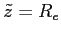 at the earth's center,
at the earth's center,
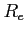 represents the earth's radius,
represents the earth's radius,
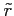 is the distance traveled along a circular arc at the sea level,
and
is the distance traveled along a circular arc at the sea level,
and
Orlando Camargo Rodríguez
2012-06-21