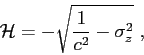Within the context of the Hamiltonian formalism the travel time can be written as
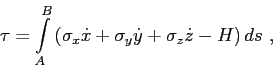 |
(A.18) |
where 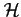 represents the system's Hamiltonian:
represents the system's Hamiltonian:
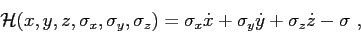 |
(A.19) |
or compactly, in vector notation:
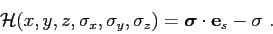 |
(A.20) |
The perturbation in travel time becomes
where
It follows then that
where
Let us notice now that
so the perturbation in travel time becomes
According to Fermat's principle
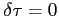 ,
which allows to infer the following system of equations
,
which allows to infer the following system of equations
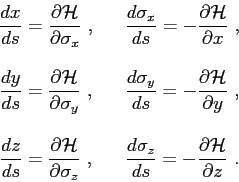 |
(A.21) |
The Hamiltonian can equally be rewritten in order to proceed with an integration along travel time,
and by substituting the components of sound slowness with the components of the wavenumber.
In fact, by taking into account that
and that
one can obtain the Hamiltonian[17]A.1:
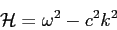 |
(A.22) |
(this expression corresponds to the Hamiltonian given by Eq.(A.19),
multiplied by the factor
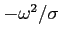 );
the system of equations becomes
);
the system of equations becomes
As shown by the two-dimensional case with cylindrical symmetry follows automatically from this case as
There are also alternativa approaches,
which consider a Hamiltonian written in terms of 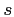 or
or 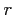 .
For the first case and for two-dimensional case with cylindrical symmetry one can obtain the Hamiltonian
.
For the first case and for two-dimensional case with cylindrical symmetry one can obtain the Hamiltonian
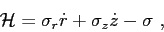 |
(A.23) |
related to the system of equations
as for the second case the Hamiltonian and associated system of equations correspond to[18]
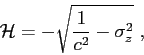 |
(A.24) |
and
Orlando Camargo Rodríguez
2012-06-21
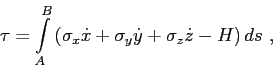
![\begin{displaymath}
\delta\tau = \displaystyle{ \int\limits_{A}^{B}} \left[
\do...
...+ \sigma_z \delta\dot{z} - \left( \ldots \right)
\right] ds
\end{displaymath}](img389.png)
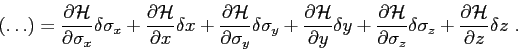
![\begin{displaymath}
\delta\tau = \displaystyle{ \int\limits_{A}^{B}}
\left[ \le...
...gma_y \delta\dot{y} + \sigma_z \delta\dot{z}
\right] ds .
\end{displaymath}](img391.png)
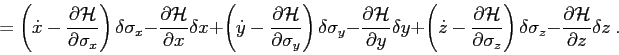
![\begin{displaymath}
\delta\tau = \displaystyle{ \int\limits_{A}^{B}}
\left[
\b...
...}
\right) \delta z \phantom{+}
\end{array} \right] ds .
\end{displaymath}](img396.png)
![]() or
or ![]() .
For the first case and for two-dimensional case with cylindrical symmetry one can obtain the Hamiltonian
.
For the first case and for two-dimensional case with cylindrical symmetry one can obtain the Hamiltonian