


Next: Gaussian beams and dynamic
Up: Theoretical background
Previous: Theoretical background
Contents
For a system with cylindrical symmetry the Eikonal equations can be written as [1]
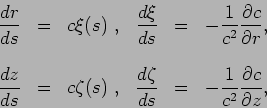 |
(1) |
where 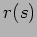 and
and 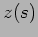 represent the ray coordinates in cylindrical coordinates
and
represent the ray coordinates in cylindrical coordinates
and 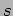 is the arclenght along the ray;
the pair
is the arclenght along the ray;
the pair
![$c(s)\left[ \xi(s),\zeta(s) \right] $](img6.png) represents the tangent versor along the ray.
Snell's law
represents the tangent versor along the ray.
Snell's law
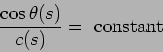 |
(2) |
follows from the second equation in the case of ray propagation with a sound speed profile (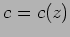 )
and flat waveguide boundaries.
)
and flat waveguide boundaries.
Initial conditions for 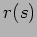 ,
, 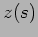 ,
, 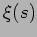 and
and 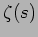 are
are
where 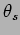 represents the launching angle,
represents the launching angle,
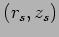 is the source position,
and
is the source position,
and 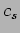 is the sound speed at the source position.
The coordinates are sufficient to obtain the ray travel time:
is the sound speed at the source position.
The coordinates are sufficient to obtain the ray travel time:
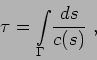 |
(3) |
which is calculated along the curve
![$\left[ r(s),z(s) \right] $](img16.png) .
.



Next: Gaussian beams and dynamic
Up: Theoretical background
Previous: Theoretical background
Contents
Orlando C. Rodriguez
2008-06-03
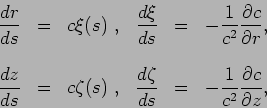
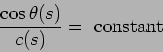
![]() ,
, ![]() ,
, ![]() and
and ![]() are
are