


Next: Boundary reflections and caustics
Up: Theoretical background
Previous: The Eikonal equations
Contents
Under the Gaussian approximation the acoustic pressure along a ray beam is defined as [2,3]
![\begin{displaymath}
P(s,n) = A \sqrt{ \frac {c(s)}{ r q(s) } } \times \exp\left[...
...a \left( \tau(s) + \frac {p(s)}{2q(s)}n^2 \right) \right] ,
\end{displaymath}](img17.png) |
(4) |
where 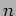 represents the normal distance from the central ray and
represents the normal distance from the central ray and 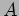 is an arbitrary constant,
which can be fixed using an expansion of a point source into beams.
After substitution into the Helmholtz equation one can obtain
the dynamic ray equations [1,4,5]
is an arbitrary constant,
which can be fixed using an expansion of a point source into beams.
After substitution into the Helmholtz equation one can obtain
the dynamic ray equations [1,4,5]
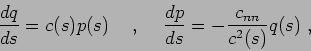 |
(5) |
where [2]
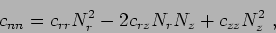 |
(6) |
and
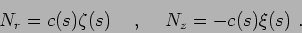 |
(7) |
Initial conditions for 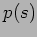 and
and 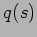 can be
can be
Thus,
the acoustic pressure along the ray can be calculated as
![\begin{displaymath}
P(s) = \phi_r \frac {A(s)}{\sqrt{r(s)}} e^{ -i\left[ \omega \tau(s) - \phi_c \right] } ,
\end{displaymath}](img27.png) |
(8) |
where the amplitude is given by [5]
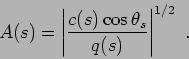 |
(9) |
The factor
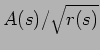 represents the ray amplitude due to cylindrical spreading;
it should be multiplied by the decaying factor
represents the ray amplitude due to cylindrical spreading;
it should be multiplied by the decaying factor 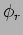 in order to account for the loss of energy due to boundary
reflections;
the factor
in order to account for the loss of energy due to boundary
reflections;
the factor 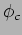 represents the shift caused by the formation of caustics.
Both
represents the shift caused by the formation of caustics.
Both 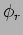 and
and 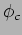 are described in the following subsection.
are described in the following subsection.



Next: Boundary reflections and caustics
Up: Theoretical background
Previous: The Eikonal equations
Contents
Orlando C. Rodriguez
2008-06-03
![\begin{displaymath}
P(s,n) = A \sqrt{ \frac {c(s)}{ r q(s) } } \times \exp\left[...
...a \left( \tau(s) + \frac {p(s)}{2q(s)}n^2 \right) \right] ,
\end{displaymath}](img17.png)
![\begin{displaymath}
P(s,n) = A \sqrt{ \frac {c(s)}{ r q(s) } } \times \exp\left[...
...a \left( \tau(s) + \frac {p(s)}{2q(s)}n^2 \right) \right] ,
\end{displaymath}](img17.png)
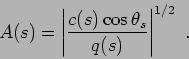
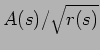 represents the ray amplitude due to cylindrical spreading;
it should be multiplied by the decaying factor
represents the ray amplitude due to cylindrical spreading;
it should be multiplied by the decaying factor