


Next: Acoustic pressure outside the
Up: Theoretical background
Previous: Gaussian beams and dynamic
Contents
In Eq.(8) the factor 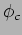 represents the phase shift induced by caustics,
which can be written as
represents the phase shift induced by caustics,
which can be written as
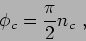 |
(10) |
where 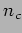 is the number of times that there is a sign change in
is the number of times that there is a sign change in 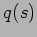 [4].
The reflection decay is given by
[4].
The reflection decay is given by
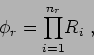 |
(11) |
where 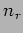 represents the total number of reflections and
represents the total number of reflections and 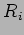 is the reflection coefficient.
Surface reflections are characterized by either
is the reflection coefficient.
Surface reflections are characterized by either 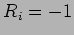 (vacuum over surface)
or
(vacuum over surface)
or 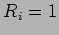 (rigid over surface).
Bottom reflections are characterized by a complex reflection coefficient,
which depends on frequency
(rigid over surface).
Bottom reflections are characterized by a complex reflection coefficient,
which depends on frequency
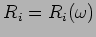 .
With
.
With 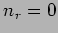 there is no decay in either phase or amplitude due to reflections,
which implies that
there is no decay in either phase or amplitude due to reflections,
which implies that 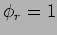 .
.
Orlando C. Rodriguez
2008-06-03