


Next: Transmission loss
Up: Theoretical background
Previous: Boundary reflections and caustics
Contents
The acoustic pressure outside the beam is calculated using geometric beams
[4,5]
![\begin{displaymath}
P(s,n) = \phi_r \frac {A(s)}{\sqrt{r(s)}} \phi(s,n) e^{ -i\left[ \omega \tau(s,n) - \phi_c \right] } ,
\end{displaymath}](img42.png) |
(12) |
where 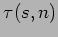 is calculated through linear interpolation,
as described in [2],
is calculated through linear interpolation,
as described in [2],
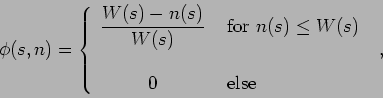 |
(13) |
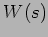 represents the beam width,
defined as
represents the beam width,
defined as
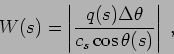 |
(14) |
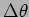 is the angular separation between the rays and
is the angular separation between the rays and
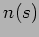 is the normal distance from the receiver coordinates
is the normal distance from the receiver coordinates 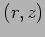 to the ray coordinates
to the ray coordinates
![$\left[ r(s),z(s) \right] $](img16.png) .
The acoustic pressure induced by
.
The acoustic pressure induced by 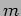 rays is the superposition of the acoustic pressure
induced by each ray:
rays is the superposition of the acoustic pressure
induced by each ray:
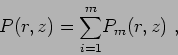 |
(15) |
where
![\begin{displaymath}
P_m(r,z) = \phi_r^m \frac {A_m(s)}{\sqrt{r}} \phi_m(s,n) e^{-i\left[ \omega \tau_m(s,n) - \phi_c^m \right] } .
\end{displaymath}](img52.png) |
(16) |



Next: Transmission loss
Up: Theoretical background
Previous: Boundary reflections and caustics
Contents
Orlando C. Rodriguez
2008-06-03
![\begin{displaymath}
P(s,n) = \phi_r \frac {A(s)}{\sqrt{r(s)}} \phi(s,n) e^{ -i\left[ \omega \tau(s,n) - \phi_c \right] } ,
\end{displaymath}](img42.png)
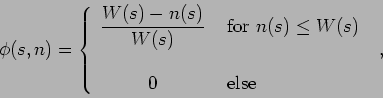
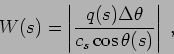
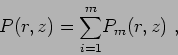
![\begin{displaymath}
P_m(r,z) = \phi_r^m \frac {A_m(s)}{\sqrt{r}} \phi_m(s,n) e^{-i\left[ \omega \tau_m(s,n) - \phi_c^m \right] } .
\end{displaymath}](img52.png)