The laws of specular reflection simply state that the angle of reflection should be equal to
the angle of incidence,
and that the incident ray,
together with the surface normal and the reflected ray,
should all lie in a common plane.
Implementing such statement in terms of angles can become quite inefficient if one keeps in mind that
the boundary is not necessarily flat;
in such case the calculation of the angles of incidence and reflection requires calculating ray and boundary slopes,
using inverse trigonometric functions to get the ray/boundary angles relative to the horizontal,
and figuring out how to combine them.
Such approach can become quite cumbersome.
An efficient method for the calculation of ray reflection consists in using the expression
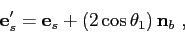 |
(5.19) |
where
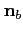 represents the boundary's normal at the point of incidence,
represents the boundary's normal at the point of incidence,
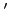 stands for the values after reflection,
and
stands for the values after reflection,
and
Thus,
every time a ray intersects a boundary,
TRACEO calculates the point of ray-boundary intersection,
which becomes the point of incidence;
the coordinates of the point are used to calculate the boundary's normal,
and Eq.(5.19) is applied;
the integration of the Eikonal equation is then restarted at the point of incidence
(as if the source was now located at the boundary),
with the launching angle being defined by the components of
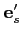 .
.
Orlando Camargo Rodríguez
2012-06-21