Besides the integration of the dynamic equations,
and the update of 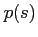 and
and 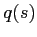 after reflections,
TRACEO borrows from Bellhop an undocumented correction of refraction,
which can be written as
after reflections,
TRACEO borrows from Bellhop an undocumented correction of refraction,
which can be written as
where 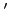 stands for the corrected value,
stands for the corrected value,
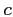 represents the sound speed at the arrival position,
and
represents the sound speed at the arrival position,
and
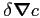 represents the ``jump'' of the gradient,
i.e., the variation of
represents the ``jump'' of the gradient,
i.e., the variation of
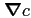 between the initial and final positions.
between the initial and final positions.
Orlando Camargo Rodríguez
2012-06-21