Theoretically,
in order to calculate the ray influence as accurately as possible the vector
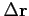 (see section 5.1)
is required to be perpendicular to the polarization vector
(see section 5.1)
is required to be perpendicular to the polarization vector
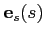 (or, alternatively, parallel to
(or, alternatively, parallel to
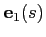 ).
For an arbitrary position of the hydrophone such condition implies traveling along the ray,
until the condition
).
For an arbitrary position of the hydrophone such condition implies traveling along the ray,
until the condition
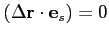 is fullfiled.
In such case the normal corresponds to
is fullfiled.
In such case the normal corresponds to
Numerical calculations indicate that there is no significant loss of accuracy
(and requires much less computations) to take
(i.e., at each hydrophone range one interpolates ray depth,
so
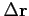 becomes a vertical vector,
connecting the ray to the hydrophone)
and to calculate the normal as
becomes a vertical vector,
connecting the ray to the hydrophone)
and to calculate the normal as
Orlando Camargo Rodríguez
2012-06-21
![\begin{displaymath}
\Delta\mbox{$\mathbf{r}$}=
\left[
\begin{array}{c}
0 \\
z_h - z(s)
\end{array} \right] ,
\end{displaymath}](img264.png)