The solution of the Eikonal equation allows to calculate the Jacobian 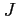 ,
between the usual set of cartesian coordinates
,
between the usual set of cartesian coordinates 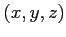 and a particular set of ray coordinates
and a particular set of ray coordinates
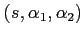 ,
where
,
where 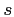 stands for the ray arclenght and
stands for the ray arclenght and 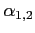 stand for some sort of auxiliary ray angles.
In general,
stand for some sort of auxiliary ray angles.
In general,
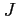 represents the cross section of a ray tube propagating from the source to the receiver.
Let us define
represents the cross section of a ray tube propagating from the source to the receiver.
Let us define
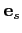 as the unitary vector tangent to the ray:
as the unitary vector tangent to the ray:
![\begin{displaymath}
\mbox{$\mathbf{e}$}_s =
\left[
\begin{array}{c}
dx/ds \\
dy/ds \\
dz/ds
\end{array} \right] .
\end{displaymath}](img78.png) |
(2.26) |
Therefore,
the first term in the transport equation, combined with the Eikonal equation,
can be rewritten as
As for the second term,
let us notice that the analytical properties of the Jacobian[3] allow to write that
The previous expressions transform the transport equation into
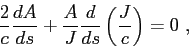 |
(2.27) |
which can be easily integrated to provide the result
where 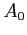 stands for a constant,
which depends of the type of acoustic source.
The solution to the wave equation can then be written as
stands for a constant,
which depends of the type of acoustic source.
The solution to the wave equation can then be written as
In the proximity of a point source one can identify the ray coordinates
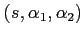 with
the spherical coordinates
with
the spherical coordinates
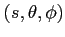 ,
centered at the source position (see Fig.2.2);
therefore, it can be written that
,
centered at the source position (see Fig.2.2);
therefore, it can be written that
with 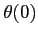 standing for the launching angle.
On the oher side, close to the source,
the acoustic field can be approximated as a spherical wave,
which implies that
standing for the launching angle.
On the oher side, close to the source,
the acoustic field can be approximated as a spherical wave,
which implies that
it follows from this relationship that
Figure 2.2:
Ray coordinates in the proximity to the source.
|
![\includegraphics[height=70mm]{sphecoor}](img89.png) |
The classical solution can then be written explicitely as
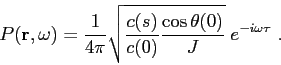 |
(2.28) |
Unfortunately,
the classical solution based on the Jacobian suffers from a serious drawback.
Each time a ray tube narrows into a single point the Jacobian becomes zero
(the points at which 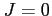 are called caustics),
and the acoustic field exhibits a singularity at such point.
Removing such singularities from the solution can be achieved by substituting the classical solution with
the solution based on Gaussian beams.
are called caustics),
and the acoustic field exhibits a singularity at such point.
Removing such singularities from the solution can be achieved by substituting the classical solution with
the solution based on Gaussian beams.
Orlando Camargo Rodríguez
2012-06-21
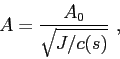
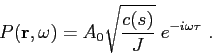
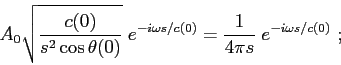
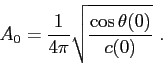
![]() are called caustics),
and the acoustic field exhibits a singularity at such point.
Removing such singularities from the solution can be achieved by substituting the classical solution with
the solution based on Gaussian beams.
are called caustics),
and the acoustic field exhibits a singularity at such point.
Removing such singularities from the solution can be achieved by substituting the classical solution with
the solution based on Gaussian beams.