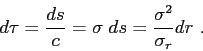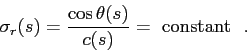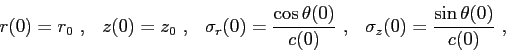Cilindrical symmetry (two-dimensional case)

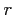In a system with cilindrical symmetry (see Fig.2.1) the Eikonal equation follows directly from Eq.(2.18) and Eq.(2.19), by replacing $x$ with $r$ and nullifying any derivative along $y$:

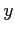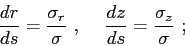$$\frac{dr}{ds} = \frac{\sigma_r}{\sigma} , \hskip5mm \frac{dz}{ds} = \frac{\sigma_z}{\sigma} ;$$ (2.21)

under this conditions the system Eq.(2.16) becomes

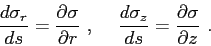$$\frac{d\sigma_r}{ds} = \frac{\partial{\sigma}}{\partial{r}} ... ...rac{d\sigma_z}{ds} = \frac{\partial{\sigma}}{\partial{z}} .$$ (2.22)

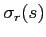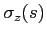In Eq.(2.22) $\sigma_r(s)$ e $\sigma_z(s)$ represent, respectively, the horizontal and vertical components of sound slowness:

$$\mbox{\boldmath$\sigma$}(s) = \left[ \sigma_r(s) , \sigma_z(s) \right] .$$

The differential of travel time can be written as

$$d\tau = \frac{ds}{c} = \sigma\; ds = \frac{\sigma^2}{\sigma_r} dr .$$

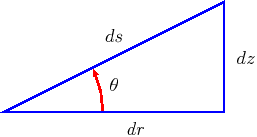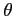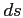Figure 2.1: Ray slope, $\theta$, ray step $ds$ and horizontal and vertical

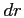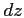steps $dr$ and $dz$ for the case of cilindrical symmetry; the parameters

are related through the following relationships:

$$dr = \cos\theta\; ds , \ dz = \sin\theta\; ds , \ \tan... ...ds = \sqrt{ \left( dr \right) ^2 + \left( dz \right) ^2 } .$$

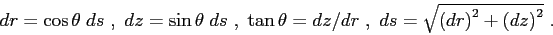
The system of equations given by Eq.(2.21) and Eq.(2.22) can be rewritten also in a more classical fashion as[3]

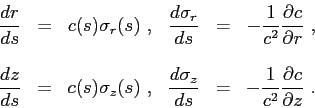$$\begin{array}{cccccc} \displaystyle{ \frac{dr}{ds} } & = & c... ...frac{1}{c^2} \frac{\partial{c}}{\partial{z}} } . \end{array}$$ (2.23)

or, more compactly, in vector form:

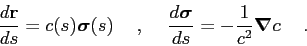$$\frac{d\mbox{$\mathbf{r}$}}{ds} = c(s) \mbox{\boldmath$\sigm... ...}{ds} = -\frac {1}{c^2} \mbox{\boldmath$\nabla$}c \hskip5mm .$$ (2.24)

When sound speed depends on depth only the horizontal slowness is preserved:

$$\frac{d\sigma_r}{ds} = 0 ;$$

this, in combination with flat boundaries, allows to infer the classical form of Snell's law along the ray:

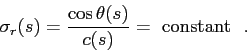$$\sigma_r(s) = \frac{\cos\theta(s)}{c(s)} = \makebox{ constant } .$$ (2.25)

The set of initial conditions required to solve the two-dimensional form of the Eikonal equation is given by

$$r(0) = r_{0} , \hskip3mm z(0) = z_{0} , \hskip3mm \si... ... , \hskip3mm \sigma_z(0) = \frac{\sin\theta(0)}{c(0)} ,$$

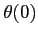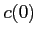where $\theta(0)$ represents the launching angle, $[r_{0},z_{0}]$ stands for the source position and $c(0)$ is the sound speed at the source position.