The Eq.(2.4) can be rewritten as
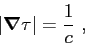 |
(2.6) |
which can be further simplified as
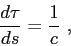 |
(2.7) |
where 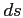 stands for the distance traveled by the acoustic wave.
Therefore, it follows that
stands for the distance traveled by the acoustic wave.
Therefore, it follows that
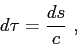 |
(2.8) |
stands for the travel time along 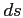 .
For a wave propagating between two points
.
For a wave propagating between two points 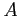 and
and 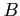 the total travel time corresponds then to
the total travel time corresponds then to
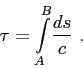 |
(2.9) |
Subsections
Orlando Camargo Rodríguez
2012-06-21