Modeling of the propagating wave would be incomplete without properly updating the values of 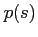 and
and 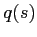 after each boundary reflection.
Following Bellhop the method used to update the values is given by:
after each boundary reflection.
Following Bellhop the method used to update the values is given by:
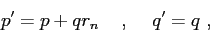 |
(5.8) |
where 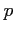 and
and 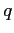 stand for the values before reflection,
and
stand for the values before reflection,
and 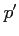 and
and 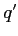 stand for the values after.
The correction
stand for the values after.
The correction 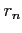 is given by the expression
is given by the expression
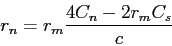 |
(5.9) |
where 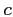 stands for the value of sound speed at the boundary,
stands for the value of sound speed at the boundary,
and
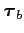 corresponds to the boundary tangent,
corresponds to the boundary tangent,
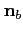 is the boundary normal and
is the boundary normal and
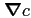 is the sound speed gradient;
additionally,
is the sound speed gradient;
additionally,
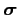 and
and
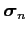 stand for the slowness and normal slowness,
which can be written as
stand for the slowness and normal slowness,
which can be written as
all parameters should be calculated at the reflection point.
Orlando Camargo Rodríguez
2012-06-21
![\begin{displaymath}
\mbox{\boldmath$\sigma$}= \frac {1}{c}
\left[
\begin{array}...
...y}{r}
-\sin\theta \\
\cos\theta
\end{array}
\right] ;
\end{displaymath}](img233.png)