The Eikonal equations (see Eq.(2.23)) are integrated by TRACEO
using a method of the Runge-Kutta type,
known as the Runge-Kutta-Fehlberg method (hereafter called RKF).
As with other Runge-Kutta methods the RKF method starts by rewriting the original system of equations,
as a linear differential vector equation
where
at each step of integration the method proceeds through a set of intermediate steps.
After each integration the RKF method provides not one,
but two different solutions.
If the solutions differe in more than a particular given threshold the ray step 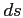 can be halved,
and the integration repeated,
providing a mean to control the accuracy of the solution.
In order to prevent an infinite loop TRACEO stops the halving (and interrupts the calculations)
if the sucessive comparisons of solutions fail to converge.
can be halved,
and the integration repeated,
providing a mean to control the accuracy of the solution.
In order to prevent an infinite loop TRACEO stops the halving (and interrupts the calculations)
if the sucessive comparisons of solutions fail to converge.
Orlando Camargo Rodríguez
2012-06-21
![\begin{displaymath}\mbox{$\mathbf{y}$}=
\left[
\begin{array}{c}
r \\
z \\
\s...
...} \\
\partial{\sigma} / \partial{z}
\end{array} \right] ;
\end{displaymath}](img235.png)