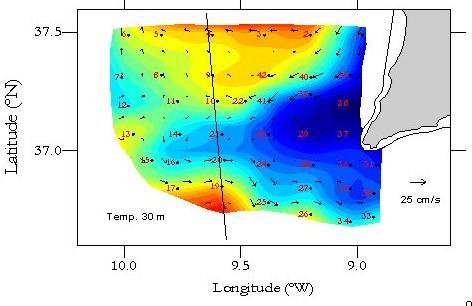
The ray solution of the Helmholtz equation represents a high frequency approximation,
which is based on the solution of the
Eikonal equation for the phase of the propagating
wave, and of the
transport equation, which accounts for the waves' amplitude.
Ray tracing models are fast to compute and allow to incorporate in a easy way the effects of
variations of sound speed and boundary variations over range. The WKBJ approximation can be further
used to construct ray-like modes of propagation. Major drawbacks of ray models are related to the
breakdown of the solution in the vicinity of focal points and caustics and also due to being unable
to handle diffraction.
Normal modes
Normal mode models expand the solution of the Helmholtz equation on an orthogonal basis of eigenfunctions,
which are obtained by solving the so-called
normal mode equation. In general each mode represents
a pair of opposite oblique waves, with a vertical component which is a standing wave and a horizontal
component which propagates away from the source. Those modes can be grouped in two categories:
- Trapped modes: modes, whose energy does not leave the boundaries of the wave-guide.
- Evanescent modes: modes, with an amplitude which decreases exponentially along range.
The normal mode expansion of the pressure field is valid as long as sound speed does not depend on range;
otherwise, the solution of the Helmholtz equation requires solving the normal mode equation at different
ranges and matching of the expansions along range as the wave propagates. That can be done by single
mode-to-mode coupling (a solution known as the adiabatic approximation) or by calculation of the coupling
coefficients, which is a time consuming procedure.
Fast field
An alternative to the mode expansion consists in the Fourier decomposition of the acoustic field into an
infinite set of horizontal waves, which can be evaluated numerically using the fast Fourier transform.
Such numerical solution of the Helmholtz equation lies at the basis of all fast field models, which can
be considered as an extension of normal mode models, since the normal mode expansion represents an
asymptotic approximation of the fast field integral far from the source. Fast field models provide
extremely accurate descriptions of the sound field at low and high frequencies, at short and large ranges
from the source, but at the cost of an intensive computational effort.
Parabolic equation
When the acoustic wave-guide is changing slowly with range the Helmholtz equation can be substituted by
the so-called
parabolic equation, which differs from the Helmholtz equation by only the first
derivative in the
r direction. Such substitution has the main numerical advantage that allows
an efficient integration of the solution by marching progressively along range. However, as a price to
be paid for the substitution it is important to keep in mind that every parabolic equation model provides
a solution, which is valid only within a narrow cone against the horizontal.

 BELLHOP:
part of the Acoustic Toolbox.
BELLHOP:
part of the Acoustic Toolbox.
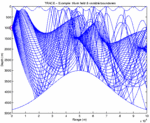
 TRACEO:
ray trace model with several options for the calculation of particle velocity and object scattering.
TRACEO:
ray trace model with several options for the calculation of particle velocity and object scattering.

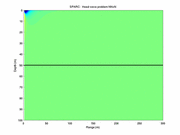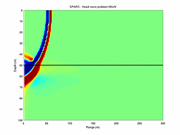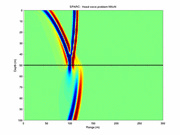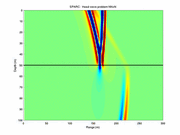
 KRAKEN:
part of the Acoustic Toolbox.
KRAKEN:
part of the Acoustic Toolbox. SNAP
SNAP
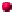 OASES
OASES SAFARI
SAFARI
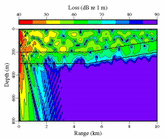
 SCOOTER: part of the Acoustic Toolbox.
SCOOTER: part of the Acoustic Toolbox.
 SAGA
SAGA